It has been some time since I’ve had a project with exciting enough results, or just exciting enough, to feature in Bob’s Research Corner. Recently, I started working on a topic that has interested me for many years. We’ve all made grids were we’ve tried to capture certain flow features. After obtaining a solution, we realized we needed more resolution in specific areas. Unfortunately time constraints by the customer do not allow us to manually refine the grid to the level that is required. This edition of Bob’s Research Corner will chronicle my attempts to develop a grid refinement utility.
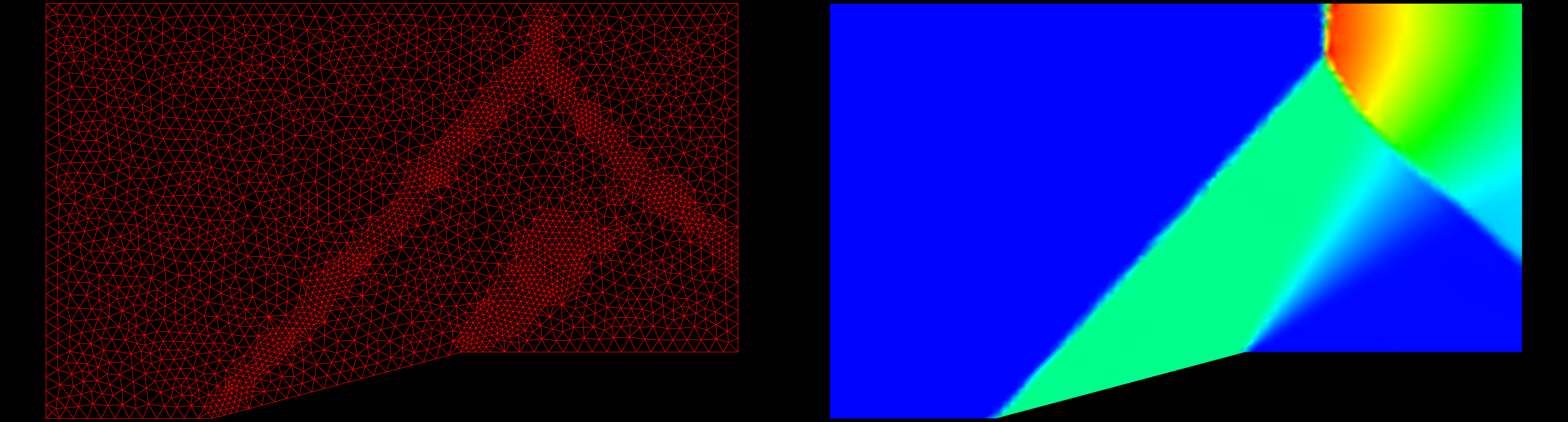
I had originally looked into grid refinement back in 2011, but shelved the project since it was low priority. At that time, I only looked a triangles and used Delaunay triangulation for refinement. I had several concerns including high aspect ratio cells and different cells types (besides triangles and tetrahedrons). Earlier this year, I focused some effort on overcoming those concerns and developed a method that might do so.
For me, grid refinement must meet three criteria:
- Refine specified features
- Make a valid grid
- Minimize the degradation of grid quality
The first criteria is relatively straight forward, although some features might get over refined while trying to target specific areas. The second criteria is probably the most difficult specifically for 3-D Boundary Layer grids and folded faces/negative volumes; the concern for 2-D is just making sure the new connectivity is correct. Lastly, care must be taken to not offset the improved solution in certain areas by degrading the grid and the solution in other areas. Initially, I will concentrate just on the first and second criterion.
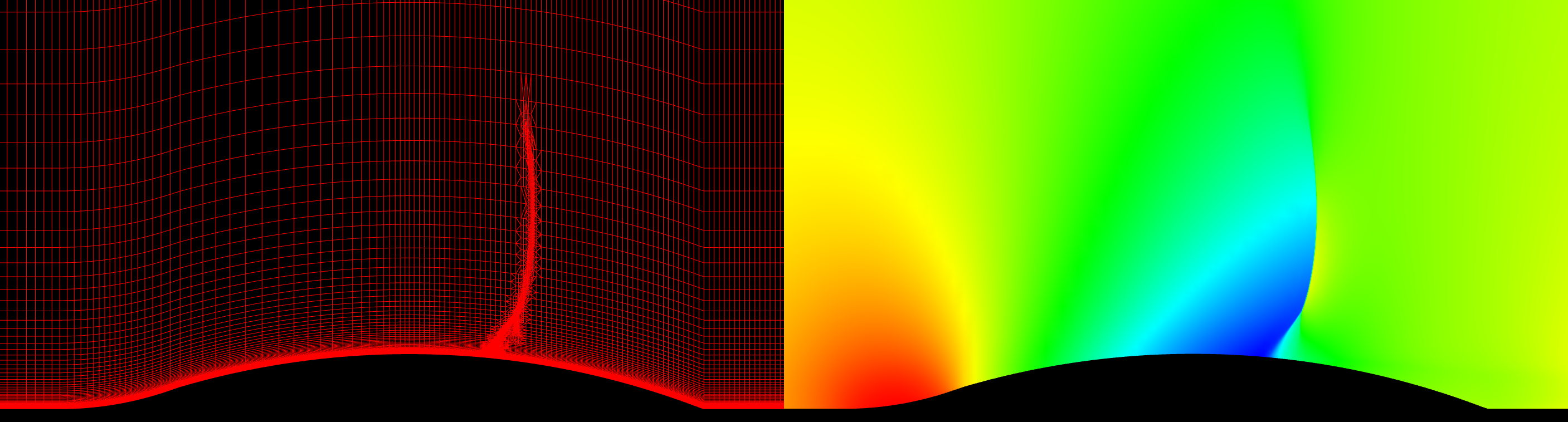
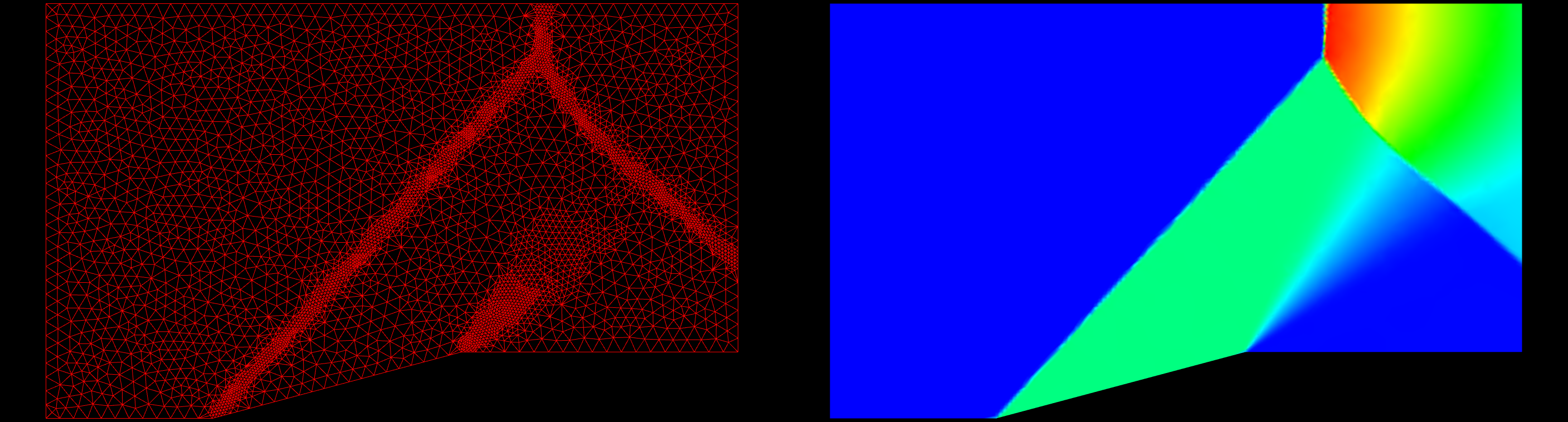
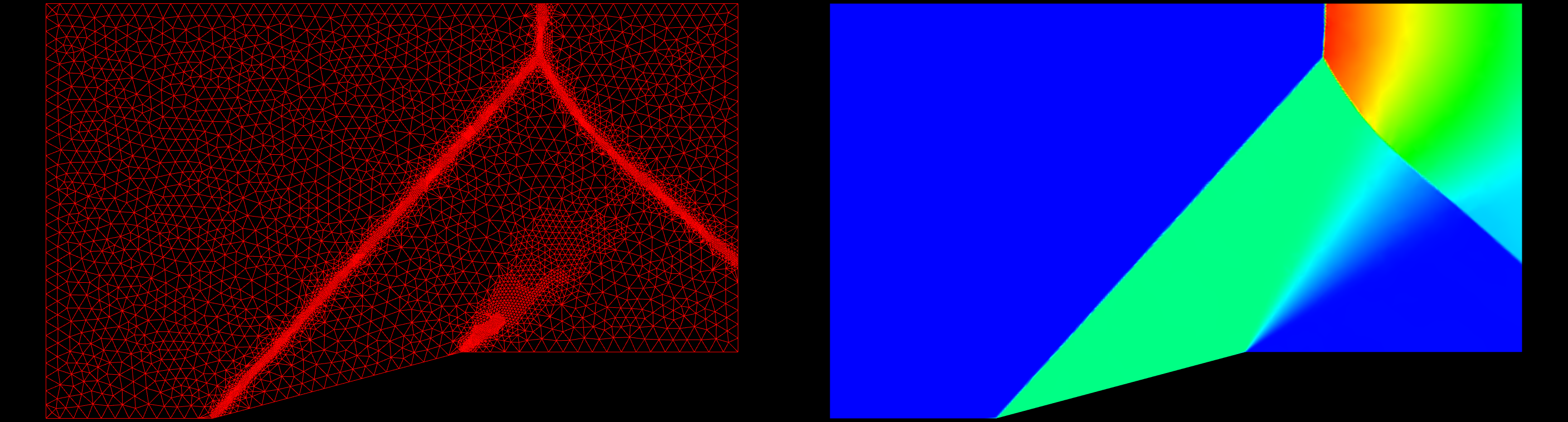
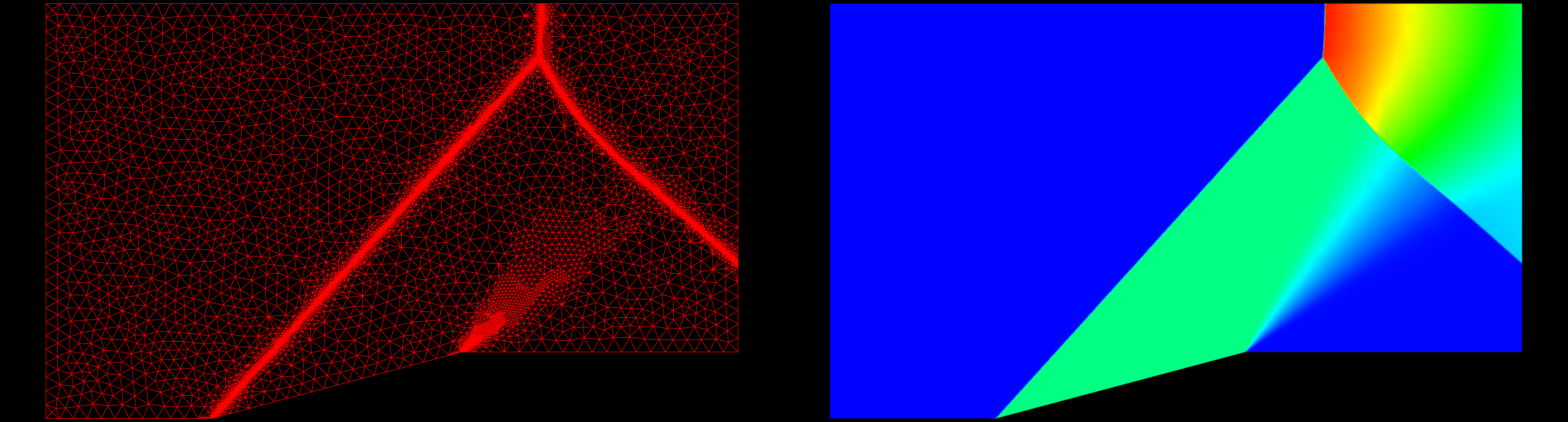
The first case I will use to test grid refinement is a supersonic ramp. The inflow Mach Number is 1.9. The solution has oblique shocks, a normal shock and an expansion fan. This is an inviscid case, and the grid contains mostly nice, equilateral triangles. A converged solution on the original grid was obtained; this solution was then used to refine the original grid. A converged solution was obtained on the refined grid. This process was repeated three more times. The slideshow below shows the grid to the left and the pressure field on the right starting with the original grid and marching to the fourth refinement. You can click on each frame to zoom in on the image. A pressure difference of 5% between cells was used as the refinement criteria.
The table below presents the statistics for the various grids. The original grid has a very high score, almost perfect, at 99.72. The fourth refinement grid results in a grid score of 96.53. There has been some degradation of the grid which must be looked into further.
| Original | Refinement 1 | Refinement 2 | Refinement 3 | Refinement 4 |
| Number of Points | 2,127 | 2,951 | 4,341 | 6,894 | 11,678 |
| Number of Faces | 6,222 | 8,686 | 12,847 | 20,498 | 34,841 |
| Number of Cells | 4,096 | 5,736 | 8,507 | 13,605 | 23,164 |
| Grid Score | 99.72 | 98.65 | 97.67 | 97.03 | 96.53 |
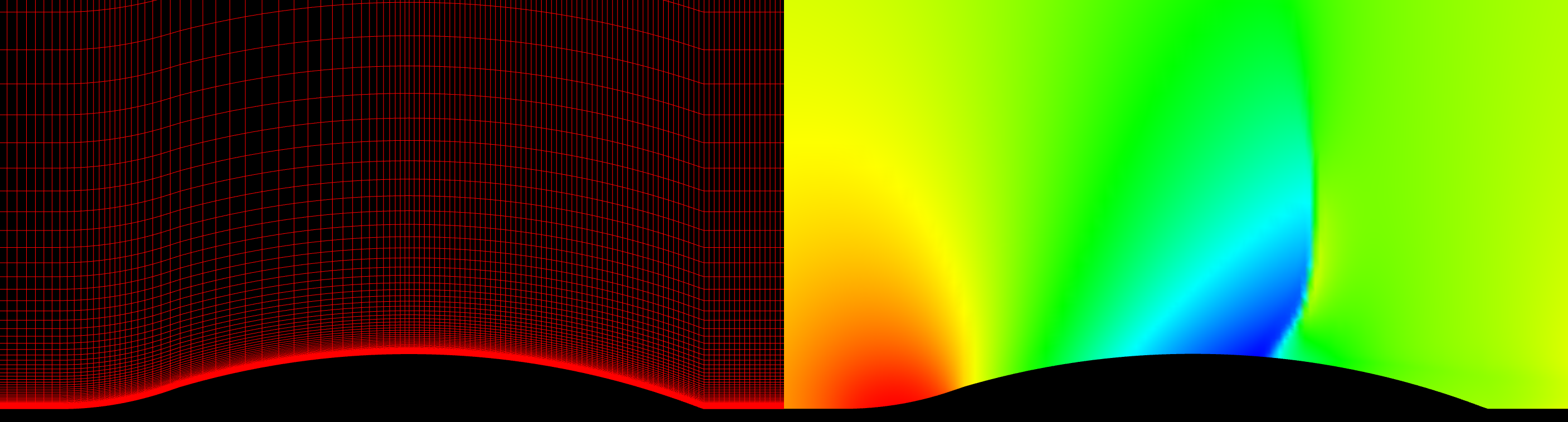
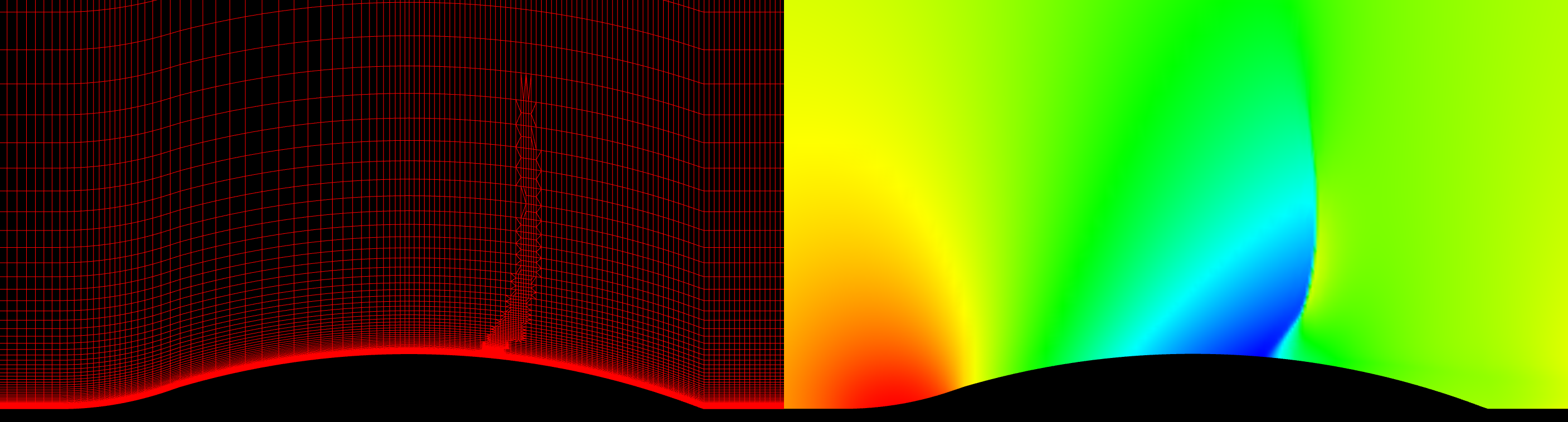
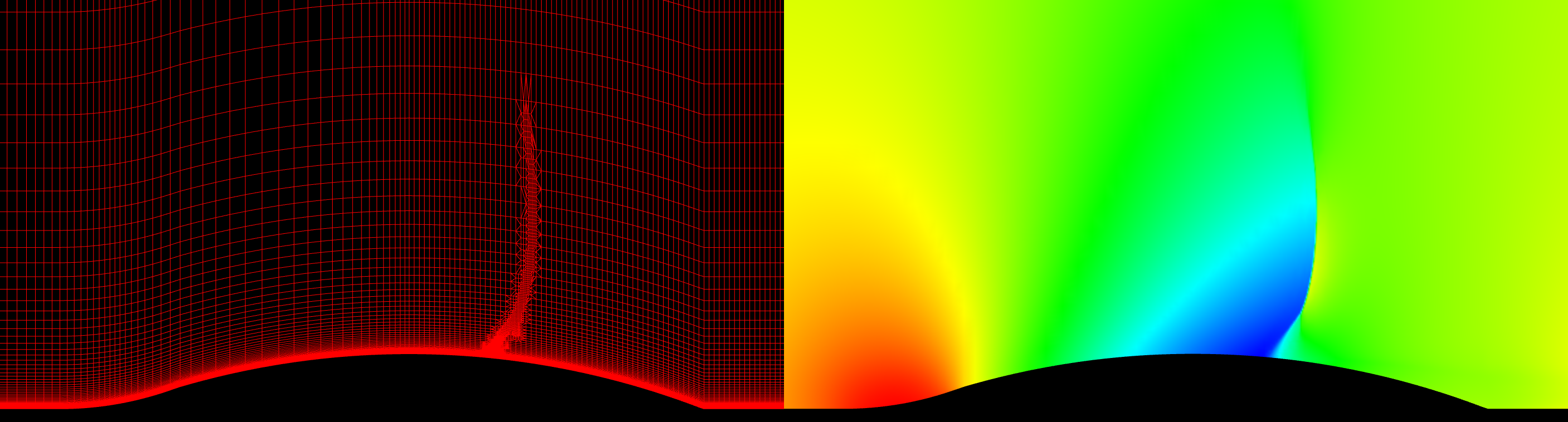
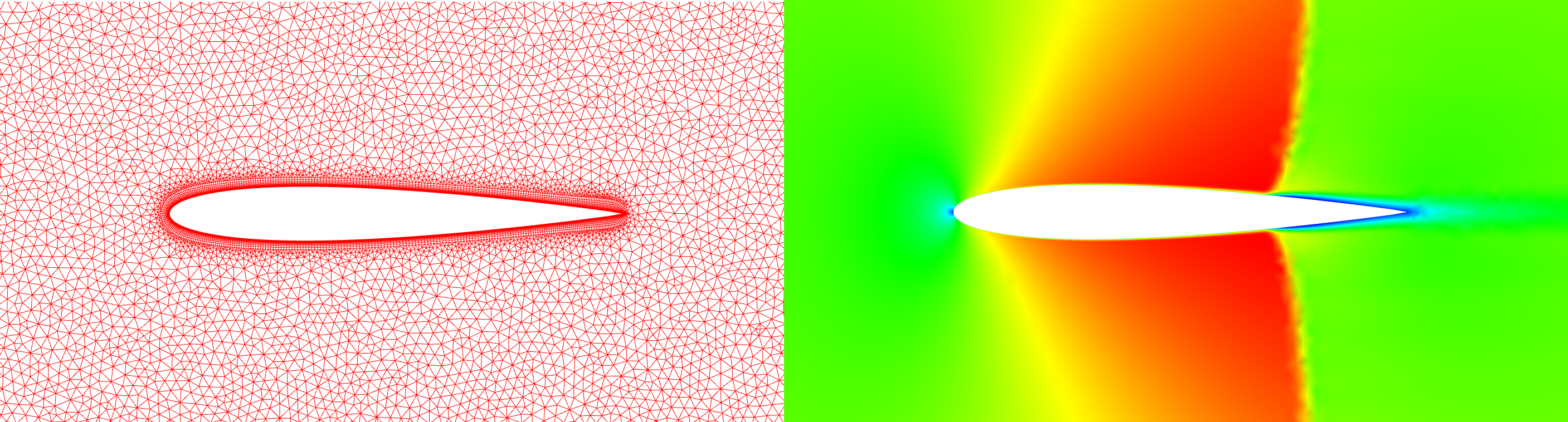
The second case is a 2-D cylinder, or circle, with a inviscid grid made up of only triangles. The incoming Mach Number is 5.0 and the Equilibrium Air model was used. The original grid was never intended for supersonic flow. It was a coarse grid for separated flow behind a cylinder. The slideshow below shows the grid on the left with the corresponding solution on the right. For this case, the flowfield is colored by density. Again, you can click on a frame to zoom in.
Grid statistics are presented in the table below. Like the Ramp, the original grid has a very high score of 99.62. The fourth refinement grid results in a grid score of 95.93.
| Original | Refinement 1 | Refinement 2 | Refinement 3 | Refinement 4 |
| Number of Points | 8,499 | 11,480 | 17,145 | 27,416 | 45,816 |
| Number of Faces | 25,230 | 34,123 | 51,054 | 81,813 | 136,982 |
| Number of Cells | 16,731 | 22,643 | 33,909 | 54,397 | 91,166 |
| Grid Score | 99.62 | 98.58 | 97.48 | 96.59 | 95.93 |
Check back next month when I plan to have the refinement of quadrilaterals implemented.