Cobalt

Cobalt is a fast, reliable and robust unstructured flow solver. It's scalability has been demonstrated on tens of thousand of processors. Included is a wide range of boundary conditions, turbulence models and rigid body motion types.

Algorithm

Cobalt is a parallel, implicit, cell-centered, finite-volume, unstructured flow solver.  The spatial operator is a second-order accurate TVD scheme based on Godunov's original first-order accurate, exact Riemann method.  The temporal operator is a second-order accurate implicit method with Newton sub-iterations.

  • Equation Models:
    • Euler, Laminar and Turbulent
  • Gas Models:
    • Ideal Gas, Thermally Perfect Gas and Equilibrium Air
  • Flow Viz FIle Format

Scalability

Cobalt has excellent parallel performance.  As you double your number of processors, your solution time is cut in half.  This will hold until the number of cells on each processors because relatively small.  As an example of scalability on 10,000 of processor, see the figure below.  This grid contained 49 million cells and as super-linear at 21,856 processors.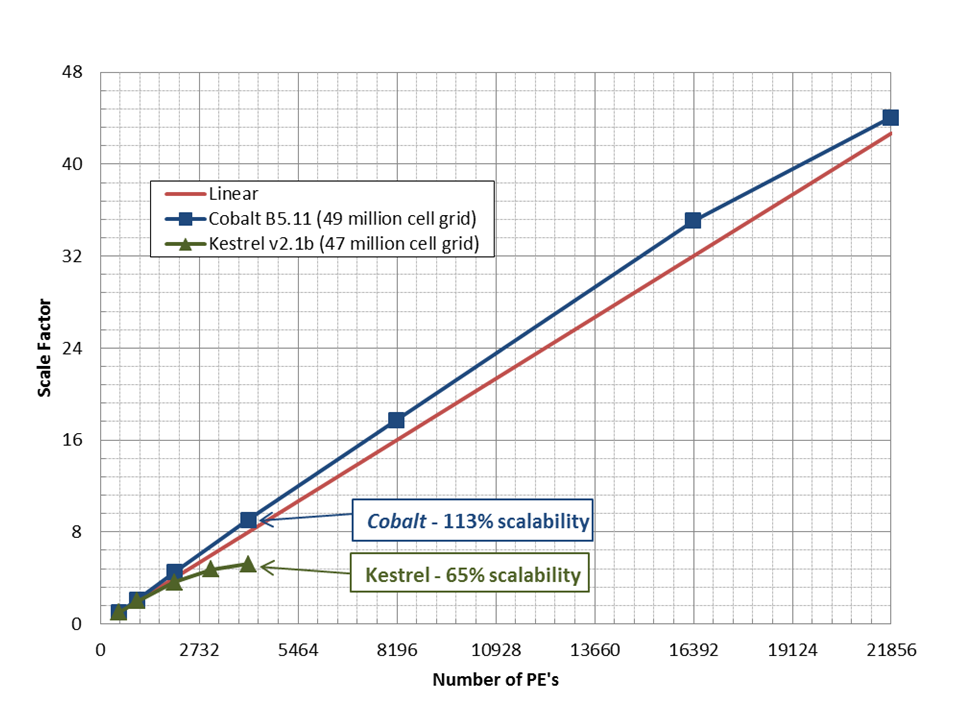scalability

Boundary Conditions

Cobalt offers a wide-range of boundary conditions.  There are nine boundary conditions types with several methods in each type.

List of Boundary Condition Types

Farfield

  • Modified Riemann Invariants
  • Modified Riemann Invariants with Random Velocity Perturbations
  • Original Riemann
  • User Profile
  • Random Velocity Perturbations
  • 2-D User Data

Solid Wall

  • Adiabatic No-Slip
  • Isothermal No-Slip
  • General No-Slip
  • 1-D Heat Equation No-Slip
  • Slip
  • Symmetry
  • Axis-of-Symmetry 

Sink

  • Static Pressure
  • Total Pressure
  • Mass Flow
  • Corrected Mass Flow
  • Mach Number
  • Valve (allows the outflow area to vary with time)

Source

  • Riemann Invariants
  • Total Pressure and Temperature
  • Mass Flow
  • Burning Grain

Rotor/Propeller

  • Disk
  • Wind Mill
  • User-Specified Wind Mill
  • Blade-Element 

Periodic

  • Linear
  • Circumferential

User

  • Specified
  • Coded

Oscillating Inflow/Outflow

  • Mass Flow
  • Velocity

Turbulence Models

Cobalt includes 24 turbulence models from one-equation RANS to DES to four equation RANS/LES hybrids.

List of Available Turbulence Models

  • Spalart-Allmaras, RANS, 1 equation
  • Spalart-Allmaras with Quadratic Constitutive Relation (QCR), RANS, 1 equation
  • Spalart-Allmaras with Quadratic Constitutive Relation from 2013 (QCR2013), RANS, 1 equation
  • Spalart-Allmaras with Delayed Detached Eddy Simulation (DDES), hybrid RANS/LES, 1 equation
  • Spalart-Allmaras with DDES and QCR, hybrid RANS/LES, 1 equation
  • Spalart-Allmaras with DDES and QCR2013, hybrid RANS/LES, 1 equation
  • Spalart-Allmaras with Rotation and Curvature Correction (SARC), RANS, 1 equation
  • SARC with QCR, RANS, 1 equation
  • SARC with QCR2013, RANS, 1 equation
  • SARC with DDES, hybrid RANS/LES, 1 equation
  • SARC with DDES and QCR, hybrid RANS/LES, 1 equation
  • SARC with DDES and QCR2013, hybrid RANS/LES, 1 equation
  • Menter Baseline (BSL), RANS, 2 equation
  • Menter Shear Stress Transport (SST), RANS, 2 equation
  • SST with DDES, hybrid RANS/LES, 2 equation
  • SST with Gamma-Theta boundary layer transition model (GT), RANS, 4 equation
  • SST-GT model with DDES, hybrid RANS/LES, 4 equation
  • SST-GT model with freestream sustainment terms, hybrid RANS/LES, 4 equation
  • SST-GT model with DDES and freestream sustainment terms, hybrid RANS/LES, 4 equation
  • SST with Scale-Adaptive Simulation (SAS), hybrid RANS/LES, 2 equation
  • Wilcox (2006) k-ω, RANS, 2 equation
  • Cobalt Solutions modified Wilcox k-ω, RANS, 2 equation
  • Hellsten Explicit Algebraic Reynolds Stress Model (EARSM), RANS, 2-equation
  • Hellsten Explicit Algebraic Reynolds Stress Model with Curvature Correction, RANS, 2 equation

Overset

Multiple grids acting as a single grid system can be simulated using our Overset module.  For more information, see Overset Module.

Rigid Body Motion

Rigid-body motions in Cobalt belong to two broad classes: ‘free’ and ‘specified’.  Free motions are those where the motion is determined by the forces and moments acting upon the body. Specified motions are those where the user specifies the motion.   With the Overset module, grids can have independent motions.

List of RBM Types

Specified

  • Oscillation
  • General Rotation and Translation
  • Arbitrary 

Free

  • 1 DoF
  • 6 DoF
  • Feedback Control (via Matlab interface)

Grid Deformation

Non-rigid body motion can be simulated using grid deformation.  For more information on our grid deformer, see Malleatus.

System Requirements

Linux (RH 6.0 or later), OpenMPI (version 1.6.5 or 1.8.4) and gfortran